1. Motivation

 

In order to get a truly deep understanding of deep neural networks, one must look at the mathematics of it. As backpropagation is at the core of the optimization process, we wanted to introduce you to it. This is denitely not a necessary part of the course, as in TensorFlow, sklearn, or any other machine learning package (as opposed to simply NumPy), will have backpropagation methods
incorporated.

 

2. The specific net and notation we will examine

 

Here’s our simple network:

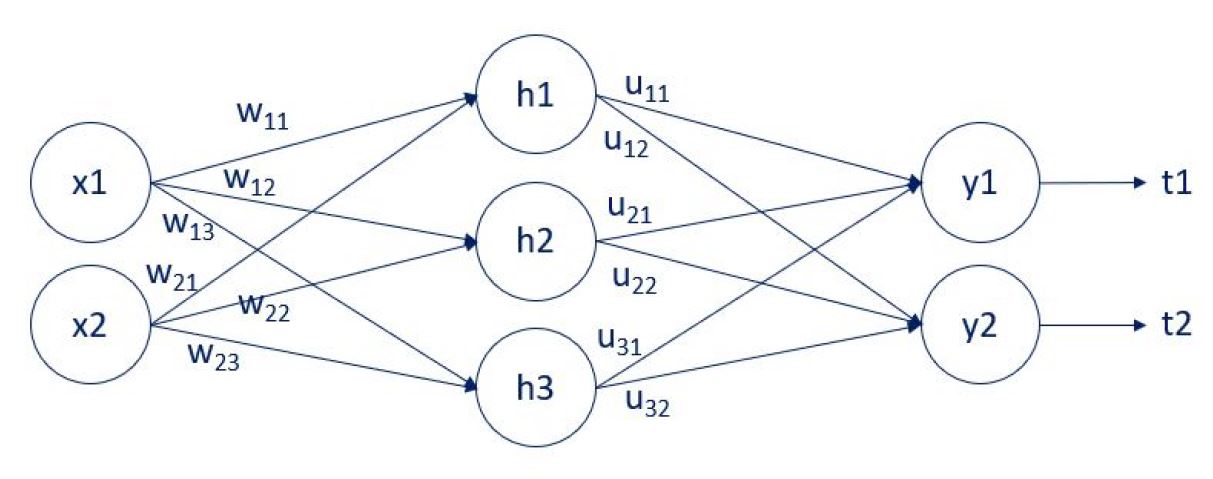Figure 1: Backpropagation

We have two inputs: x1 and x2. There is a single hidden layer with 3 units (nodes): y1, y2, and y3. Finally, there are two outputs: y1 and y2. The arrows that connect them are the weights. There are two weights matrices: w, and u. The w weights connect the input layer and the hidden layer. The u weights connect the hidden layer and the output layer. We have employed the letters w, and u, so it is easier to follow the computation to follow. You can also see that we compare the outputs y1 and y2 with the targets t1 and t2.

There is one last letter we need to introduce before we can get to the computations. Let a be the linear combination prior to activation. Thus, we have:
а(1) = xw + b(1) and a(2) = hu + b(2).
Since we cannot exhaust all activation functions and all loss functions, we will focus on two of the most common. A sigmoid activation and an L2-norm loss. With this new information and the new notation, the output y is equal to the activated linear combination. Therefore, for the output layer, we have y = σ(a(2)), while for the hidden layer: h = σ(a(1)).

We will examine backpropagation for the output layer and the hidden layer separately, as the methodologies differ.

 

3. Useful formulas

 

I would like to remind you that:

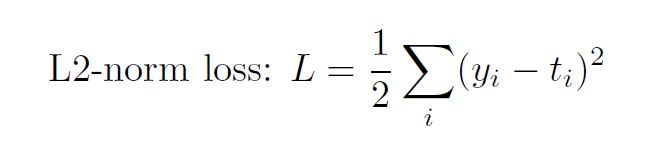
The sigmoid function is:

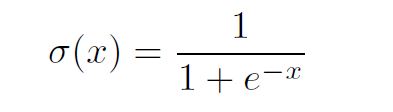
and its derivative is:

 

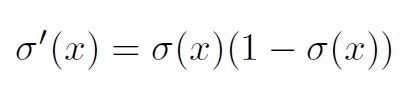
  4. Backpropagation for the output layer

 

In order to obtain the update rule:

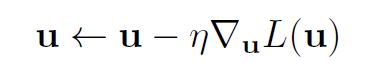
we must calculate

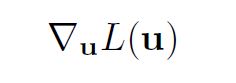
Let’s take a single weight uij . The partial derivative of the loss w.r.t. uij equals:

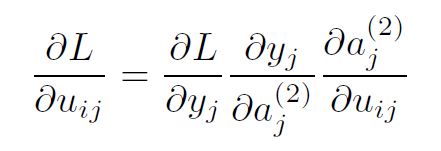
where i corresponds to the previous layer (input layer for this transformation) and j corresponds to the next layer (output layer of the transformation). The partial derivatives were computed simply following the chain rule.

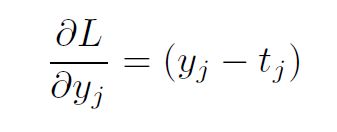
following the L2-norm loss derivative.

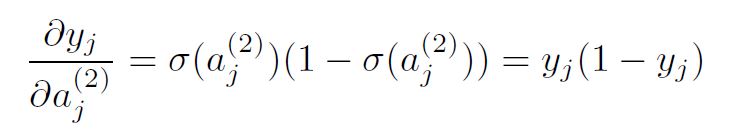
following the sigmoid derivative.

Finally, the third partial derivative is simply the derivative of a(2) = hu + b(2).

So,

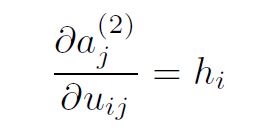
Replacing the partial derivatives in the expression above, we get:

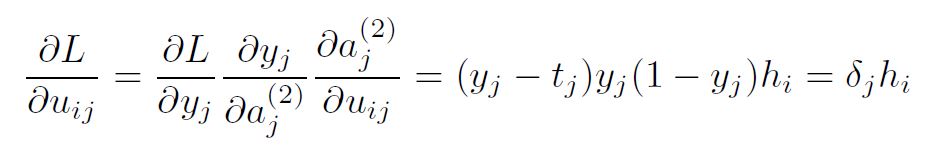
Therefore, the update rule for a single weight for the output layer is given by:

  5. Backpropagation of a hidden layer

 

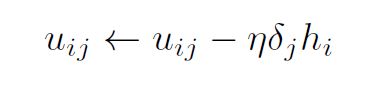
Similarly to the backpropagation of the output layer, the update rule for a single weight, wij would depend on:

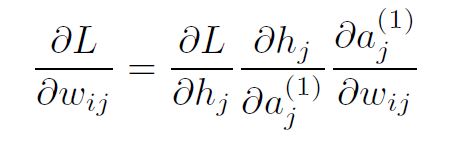
following the chain rule. Taking advantage of the results we have so far for transformation using the sigmoid activation and the linear model, we get:

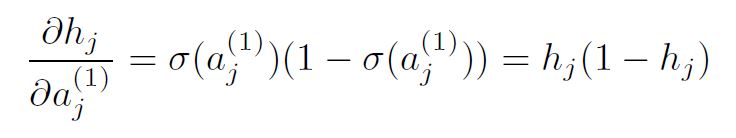
and

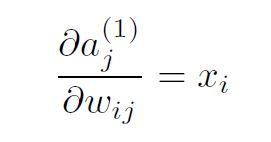
The actual problem for backpropagation comes from the term

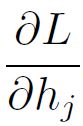
That’s due to the fact that there is no “hidden” target. You can follow the solution for weight w11 below. It is advisable to also check Figure 1, while going through the computations.

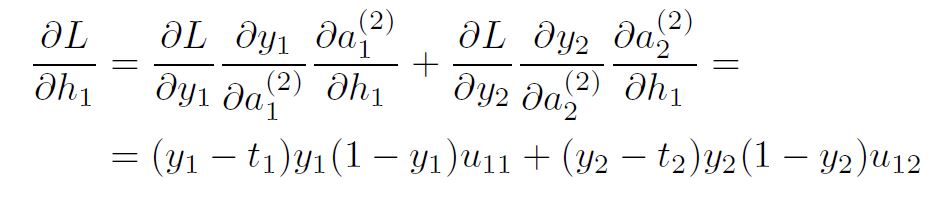
From here, we can calculate

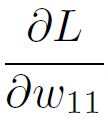
which was what we wanted. The final expression is:

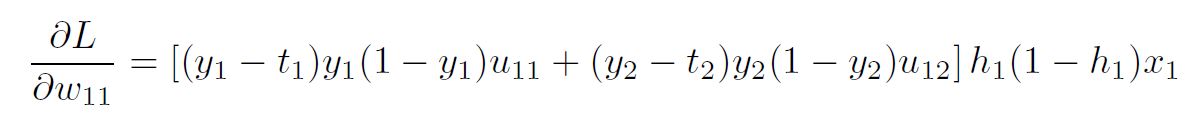
The generalized form of this equation is:

  6. Backpropagation generalization

 

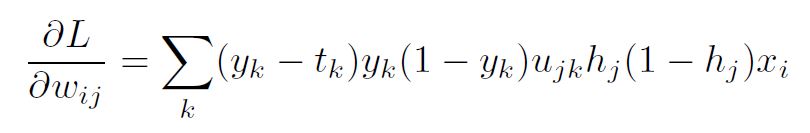
Using the results for backpropagation for the output layer and the hidden layer, we can put them together in one formula, summarizing backpropagation, in the presence of L2-norm loss and sigmoid activations.

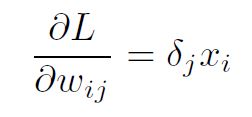
where for a hidden layer

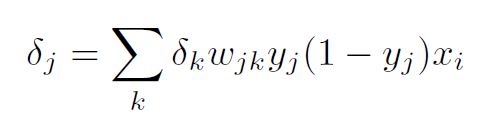
Kudos to those of you who got to the end.

Thanks for reading.